Imperative Versus Functional Programming
Imperative Programming Paradigm
Imperative (also called procedural) programming languages such as FORTRAN and C have been in use for a long time, and most engineers in the water management domain are familiar with the concepts. The structure of imperative, or statement-oriented languages is dominated by imperative statements, which, when evaluated in a given sequence, achieve the desired results of the program.
This type of language evolved as a natural extension of the Von Neumann computer architecture. Such languages are characterized by the existence of variables, the possibility of assigning values to variables, and mechanisms for repetition (iteration), mirroring the three computer architectural concepts of memory cells, storing or assigning values to memory cells, and the repetition of a set of instructions which are stored in memory.
Figure 1.1 illustrates a how an imperative programming language might be used to implement a portion of a water management policy:
Figure 1.1

In this example Inflow, Outflow, and Pool_Elevation are global variables; that is, any part of the code can read from or write values to these memory locations. The first several statements provide these memory locations with initial values. Then a subroutine is called to perform the “surcharge release” computation. We don’t know what that computation is, but we can guess that is sets Outflow and Pool_Elevation to reflect high priority policy considerations. It could do other things as well, like modify other values (e.g., Storage). Next, another routine is called which performs the “flood release” computation. Again, we don’t know what this routine does, but perhaps it might readjust the values set by the SurchargeRelease routine to manage flooding scenarios.
The use of memory locations is a key aspect of imperative programs. The two subroutines executed by the program fragment above presumably takes advantage of the memory locations corresponding to the global variables by reading them to get their values and assigning values to them.
Two advantages of the imperative programming approach are that programs tend to be efficient (because the program organization mirrors the machine architecture) and most water resources engineers are accustomed to this style of computation.
Referential Transparency
Imperative languages have a problem related to the issue of referential transparency. A system is said to be referentially transparent if the meaning of the whole can be determined solely from the meaning of its parts. Mathematical expressions are referentially transparent. Imperative languages are not referentially transparent because the value of a variable or the meaning of an expression (result of its evaluation) depends on the history of computation. Assignment statements, parameters passed by reference, and global variables are the main reasons that imperative languages are not referentially transparent. The lack of referential transparency means that it is possible to create programs which are difficult to read, modify and prove correct.
Functional Programming Paradigm
A functional language, by contrast, makes use of the mathematical properties of functions. Recall from mathematics that a function is a mapping from a set of values in some domain to a single value. Thus f(x,y,z) evaluates to a single value when specific values are given to x, y and z. A purely function programming language performs all of its computations by evaluating functions, i.e., by evaluating for various inputs the mathematical expressions which define the functions.
Notice that this description of purely functional programming languages contains no reference to memory locations. Since there is no setting of values in memory when evaluating a mathematical function, there are no hidden “side effects.” This lack of side effects allows functions to be combined hierarchically with predictable results. Knowledge of all the effects and predictability of the results makes the functional approach referentially transparent.
Let’s look at how the policy fragment from above might be written in a more functional manner:
Inflow = 100.0
Outflow = SurchargeRelease(Inflow)
Pool_Elevation = MassBalance(Inflow, Outflow)
Outflow = FloodRelease(Inflow)
Pool_Elevation = MassBalance(Inflow, Outflow)
If we allow functions to read (but not write!) global memory locations, then we don’t need to pass the inputs to the function in explicitly, and this policy fragment might be written:
Inflow = 100.0
Outflow = SurchargeRelease()
Pool_Elevation = MassBalance()
Outflow = FloodRelease()
Pool_Elevation = MassBalance()
This code is quite similar to the original code fragment, but a couple of differences from the original code are worth highlighting. First, since a function produces only one return value, the functional computation requires separate functions for computing the value of Outflow and Pool_Elevation. Thus the SurchargeRelease function now only computes Outflow, and we have introduced the MassBalance function, which uses Inflow and Outflow to compute the Pool_Elevation.
Note: This code is not strictly functional. We have retained from the original imperative program the idea of statements which assign values to memory locations, however we have moved the assignments to the outermost level. If we further stipulate that evaluating the three functions have no side effects (simply compute a value and don’t change any memory locations), then this policy fragment becomes quite easy to read and understand. That is, it is immediately obvious which portions of the policy are affecting Outflow, which Pool_Elevation, and so on.
This is the philosophy of the RPL in a nutshell: restrict the setting of global values (slot or model values) to the outermost level of policy statements, all other policy computation is via function and expression evaluation. The key aspects of function and expression evaluation are as follows:
• Functions operate on zero or more input values.
• Functions evaluate to a single value (or to a list of values, considered a single item).
• Global memory values are not affected.
The advantages of this approach are that we can easily see where and how values are computed. We can look at the functions to see what they do; there are no hidden side effects.
Examples
The purpose of the following examples is to familiarize the reader with the RPL approach to describing computation and to provide the opportunity to practice this style of problem-solving.
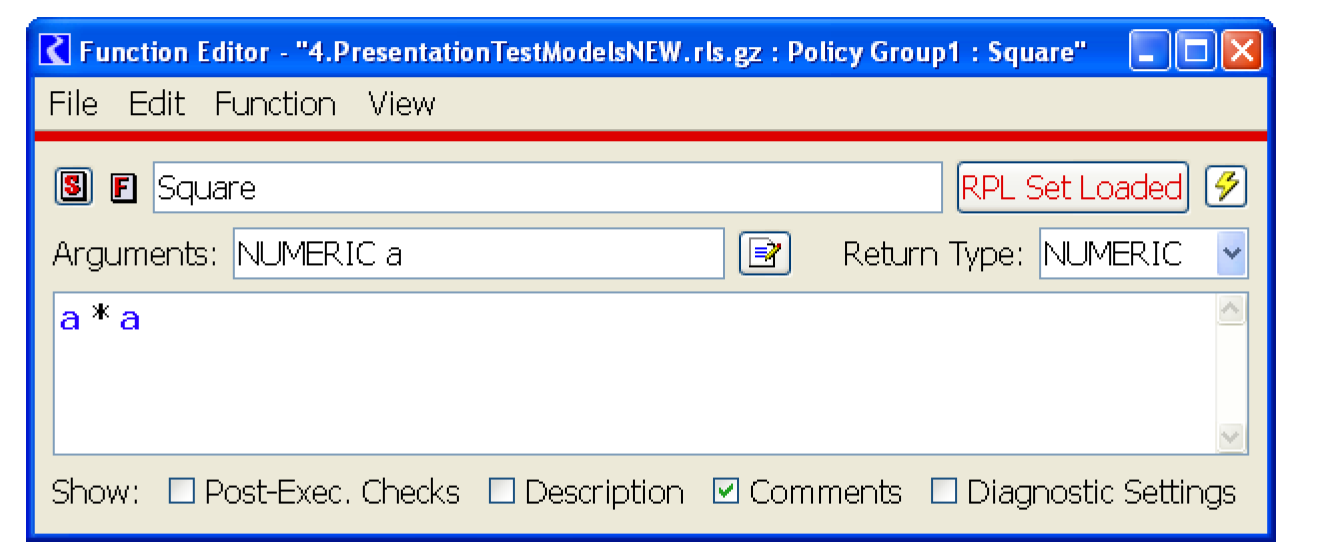
The following subroutine finds the square of a number.
SUBROUTINE Square( FLOAT a, FLOAT answer )
answer = a * a
END
Figure 1.2 shows the same program written as a RPL function.
Figure 1.2
The following imperative-style function finds the minimum of two numbers.
FUNCTION Min( FLOAT a, FLOAT b )
FLOAT answer
IF ( a < b )
answer = a
ELSE
answer = b
END IF
RETURN answer
END
Figure 1.3 shows the same function implemented within RPL.
Figure 1.3
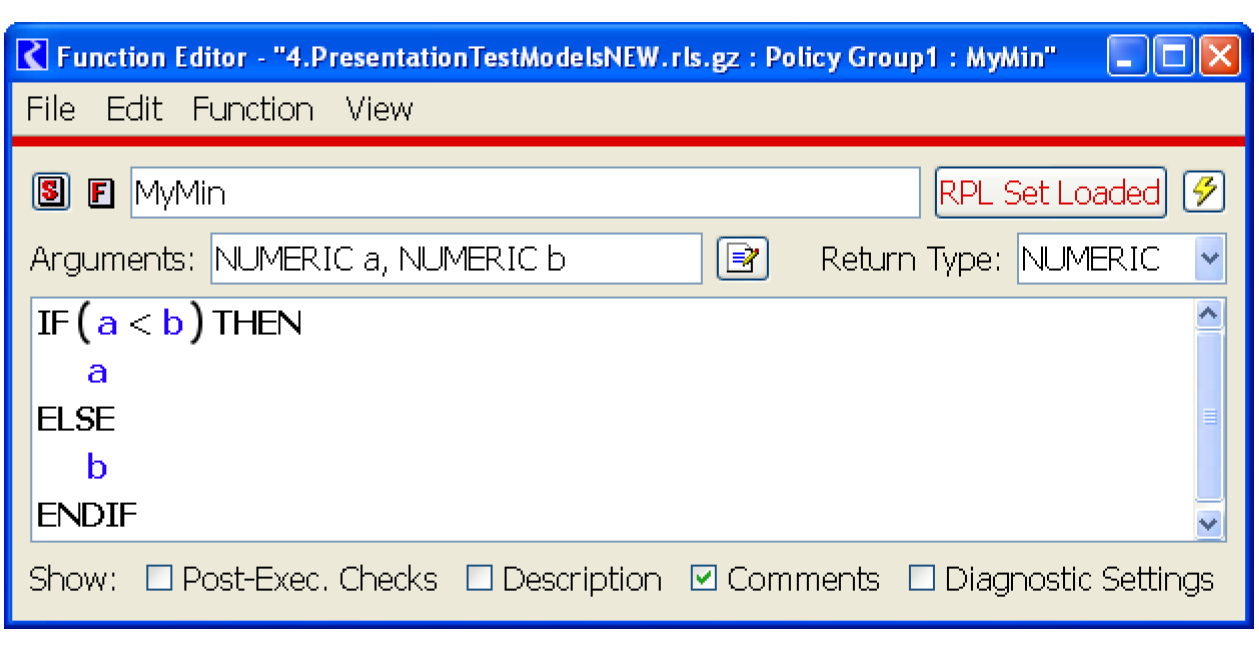
Note: The RPL IF expression evaluates to a single value, as do all functions and expressions.
The following procedure takes an array of numFlows flow values and returns the sum of these flows:
SUBROUTINE SumFlows( FLOAT ARRAY flows,INTEGER numFlows,FLOAT total )
INTEGER i = 0
total = 0
WHILE ( i < numFlows )
total = total + flows[i]
i = i + 1
END WHILE
END
Figure 1.4 shows RPL code that accomplishes the same task.
Figure 1.4
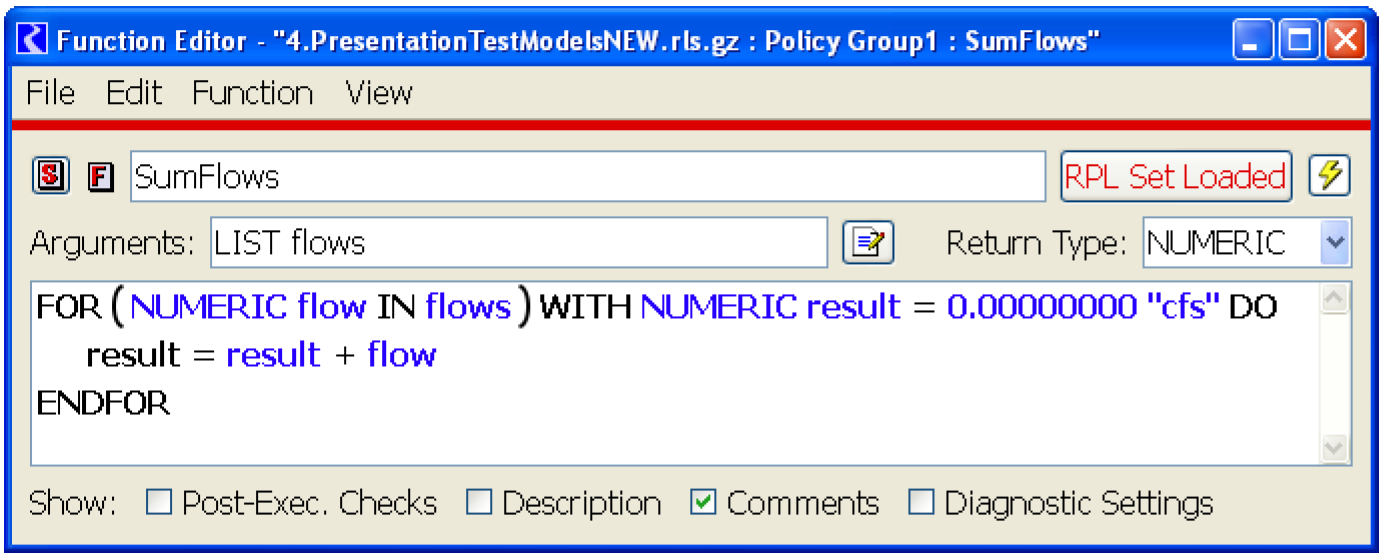
Note: The FOR expression evaluates to a single value.
Following are the steps in evaluation of a FOR expression:
1. The list expression is evaluated.
2. The initialization expression is evaluated and the result is assigned to the loop variable.
3. The first/next item in the result of evaluating the list expression is assigned to the index variable.
4. The body is evaluated and the result is assigned to the loop variables.
5. If there are more values in the result of evaluating the list expression, return to the third step.
6. Return the value of the loop variable.
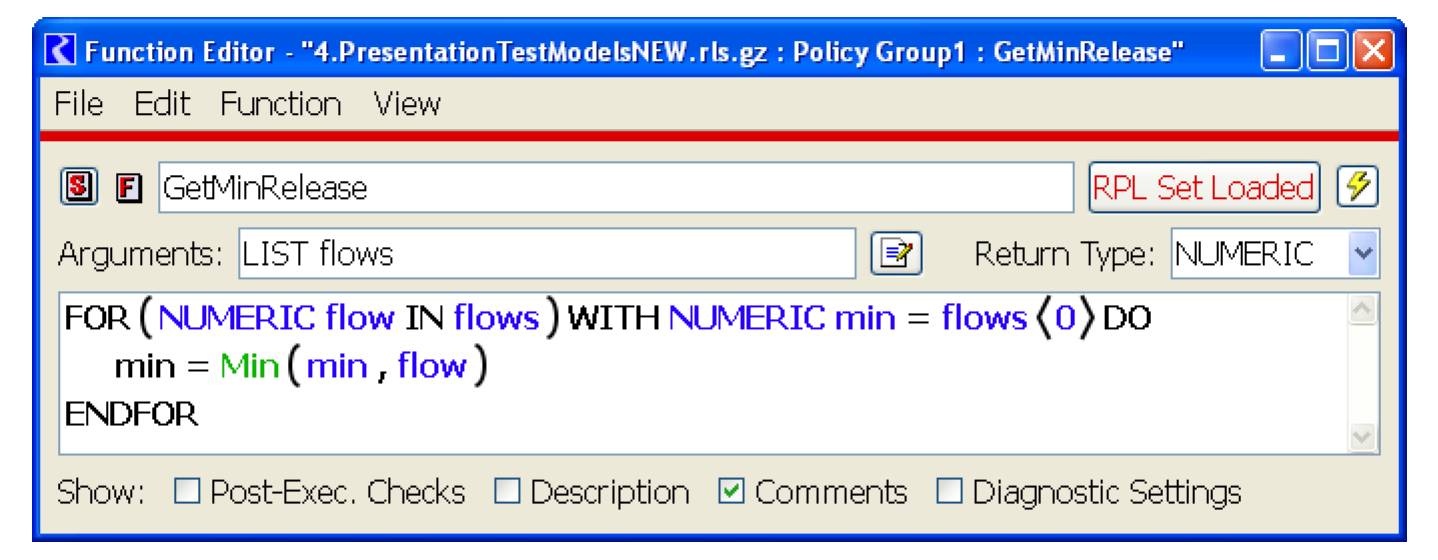
The following procedure takes an array of numFlows reservoir releases and returns the minimum of these values:
SUBROUTINE GetMinRelease( FLOAT ARRAY flows,INTEGER numFlows,FLOAT min )
min = flows[0]
INTEGER i = 1
WHILE ( i < numFlows )
IF ( min > flows[i] )
min = flows[i]
END IF
i = i + 1
END WHILE
END
The RPL version shows how iteration can be framed as an expression which evaluates to a single value (and uses the Min function defined above). Figure 1.5 illustrates.
Figure 1.5
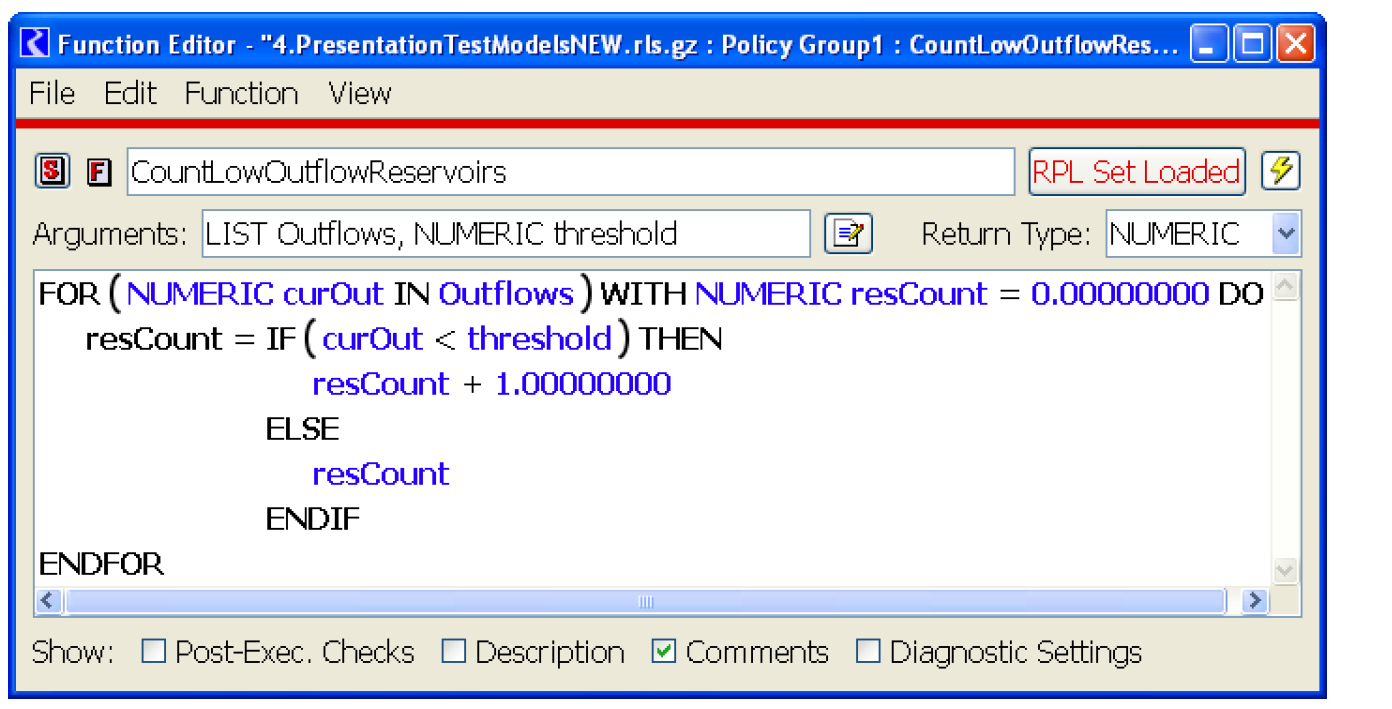
Given the pool elevation of numRes reservoirs, the following subroutine counts the number of reservoirs whose pool elevation is below a certain threshold.
SUBROUTINE CountLowReservoirs( FLOAT ARRAY PEs,INTEGER numRes,FLOAT threshold,INTEGER resCount )
resCount = 0
INTEGER i = 0
WHILE ( i < numRes )
IF ( PEs[i] < threshold )
resCount = resCount + 1
END IF
i = i + 1
END WHILE
END
Figure 1.6 shows a possible solution.
Figure 1.6
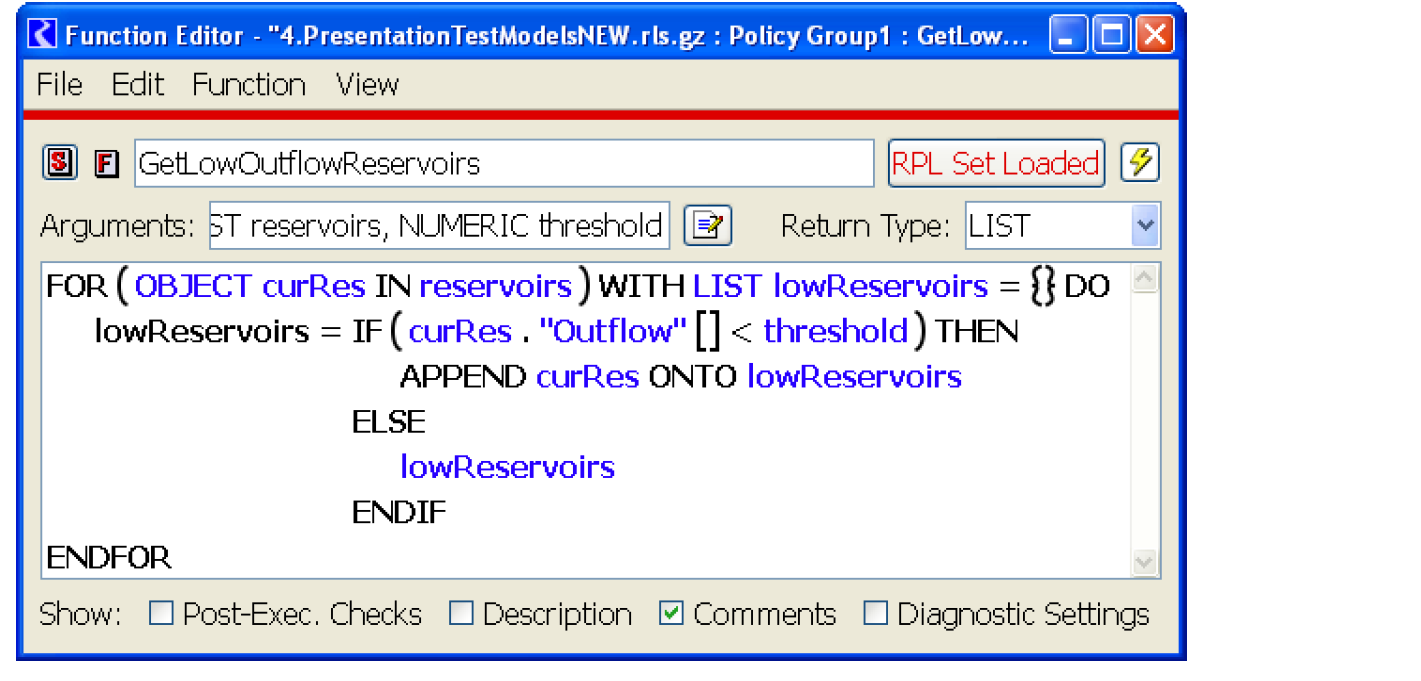
To illustrate the use of some of the RPL built-in list operations, consider a variation on the previous example, in which we would like a list of the reservoirs whose pool elevation is below a certain threshold. Figure 1.7 illustrates.
Figure 1.7
Revised: 08/02/2021