Thermal Unit Replacement Value
No evaluation is made.
The economic value of hydropower is set equal to (or replaced by) the savings from replacing generation from thermal power sources.
A constraint is added to meet the load. This load must be met (or exceeded) by a combination of the following power sources: thermal energy, power reservoir energy, allocated energy (from outside the basin), and net energy from pumped storage facilities (generation - pumping).
(5.64) 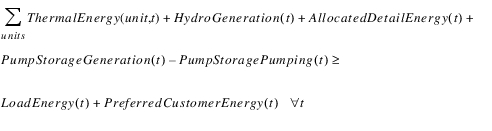
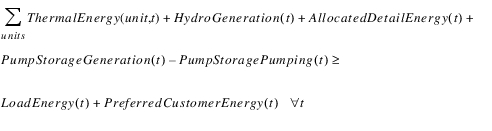
The constraint is written as an inequality, rather than an equality, to allow for piecewise linearization of power. The assumption is that an objective function will be written that will tend to maximize the energy generated for a given amount of turbine release. For example, an objective function minimizing the cost of thermal generation would be sufficient.
Additional terms are available for writing more complex objective functions. In this method, Avoided Operating Cost is defined as the reduction in the cost of thermal generation, the thermal costs of meeting the load with only thermal sources minus the cost of a combined hydropower and thermal solution.
(5.65) 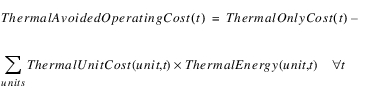
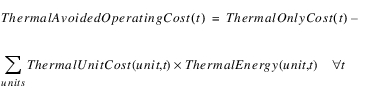
Thermal Energy is further constrained by unit capacity and availability:
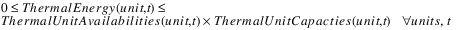
Slots Specific to This Method
See Calculate Thermal Unit Replacement Value in Objects and Methods for slot descriptions.
Revised: 08/02/2021